 | Un genre de croix |
| | Cette méthode est basée sur le principe de la croix du X-Wing. Le principe du fonctionnement est exactement le même.
|
 | Le principe |
| | Il est nécessaire de trouver 3 colonnes (ou 2 colonnes et 1 région) dans lesquelles on ne trouve que 2 candidats pour une même valeur. Et qu'en plus on retrouve cette correspondance dans 3 lignes. Pour pouvoir supprimer les autres candidats des lignes communes (sauf dans les colonnes de départ!).
Fonctionne exactement de la même façon dans l'autre sens, pour 3 lignes avec 3 colonnes en commun.
|
 | Un peu de souplesse en plus |
| | Si le principe ci-dessus reste la règle de base pour que ça puisse fonctionner. On constate que ça fonctionne de la même façon avec 3 candidats. Pour autant qu'on ne retrouve que 3 lignes en commun.
|
 | Un exemple (3 colonnes avec 3 lignes) |
| | 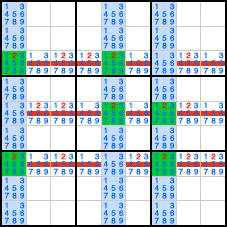
Dans cet exemple, il n'est possible de trouver le candidat "2" qu'a deux emplacements des colonnes C1, C5 et C7. De plus ces candidats font partie des 3 lignes communes à 2 colonnes L3, L5 et L7. Il est donc possible de supprimer tous les autres candidats "2" de ces 3 lignes.
|
 | Pourquoi ? |
| | Car en effet si l'on choisit le premier "2" de la première colonne (L3C1), c'est automatiquement le deuxième "2" de la deuxième colonne (L5C5) qui restera comme seul candidat, de même que le deuxième "2" de la troisième colonne (L7C7).
Et si l'on fait l'autre choix dans la première colonne (L7C1), c'est l'autre candidat de la troisième colonne qui restera (L5C7), de même que l'autre candidat de la deuxième colonne (L3C5).
C'est donc une diagonale ou l'autre, mais on ne peut pas encore savoir laquelle! La seule chose certaine, c'est que les "2" ne sont plus de bons candidats pour les autres cases de ces trois lignes (L3, L5 et L7)
|
 | Un autre exemple (3 colonnes avec 2 lignes et 1 région) |
| | 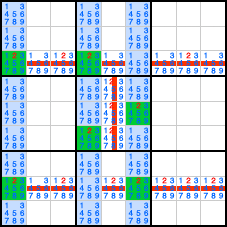
On ne trouve le candidat "2" que 2 fois dans les colonnes C1, C4 et C6, de plus dans les mêmes lignes (L3 et L8) avec une région en commun (R5) pour 2 colonnes (C4 et C6). Il est donc possible de supprimer les autres "2" des 2 lignes correspondantes et de la région.
|
 | Un dernier exemple (2 colonnes et 1 région avec 2 lignes et 2 régions) |
| | 
Toujours le même principe...
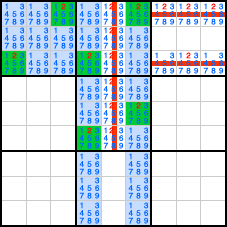
Il est facile de comprendre que dans la mesure où les unités concernées ne contiennent toutes que 2 possibilités, il faut choisir l'une ou l'autre. Et quel que soit le choix, les candidats alignés sont supprimés. Et comme eux aussi vont par deux, quand on en supprime un il reste l'autre. Et ensuite à nouveau sur les candidats alignés ou du même groupe.
|
 | Aussi pour les autres |
| | Cette méthode s'applique dans les cas suivants, avec 2 candidats:
- dans 3 colonnes, en supprimant les candidats dans 3 lignes
- dans 3 colonnes, en supprimant les candidats dans 2 lignes et 1 région
- dans 2 colonnes et 1 région, en supprimant les candidats dans 2 lignes et 2 régions
- dans 3 lignes, en supprimant les candidats dans 3 colonnes
- dans 3 lignes, en supprimant les candidats dans 2 colonnes et 1 région
- dans 2 lignes et 1 région, en supprimant les candidats dans 2 colonnes et 2 régions
|
 | Utilisation |
| | Il est possible d'utiliser cette méthode dans toutes les lignes ou colonnes, en liaison avec toutes les autres unités
|
 | Exemples |
| |
|
 | Variantes |
| | D'autres techniques utilisent exactement le même principe:
- X-Wing (2 candidats dans 2 unités communes)
- Jellyfish (2-4 candidats dans 4 unités communes)
- Squirmbag (2-5 candidats dans 5 unités communes)
- Burma (3 candidats dans 3 unités communes)
|